Nekorektní blog Petra Kubáče na Blog.cz

Abychom se nemuseli otravovat s velikými čísly - předpokládejme že 4 bitový procesor zpracovává 4 bitový signál.

4 bitový signál - pokud jej bereme jako "číslo bez znaménka" alias Unsigned Integer - nabývá binárních hodnot 0000 - 1111 tedy 0-15. Pokud jej bereme jako Signed Integer - tedy "číslo se znaménkem" - nabývá hodnot 1000 - 0111 tedy -8 až +7.

Protože Unsigned integer je nejjednodušší - předpokládejme že počítáme s nimi - a že sčítáme 9+9 - což jsou obě zcela legální 4 bitová čísla. jejich součet je 18 a to už není legální 4 bitové číslo. Pokud si to napíšeme binárně je to 1001 + 1001 = 10010. Jenomže náš procesor je jenom 4 bitový takže z jeho pohledu 1001 + 1001 = 0010 neboli 9+9 = 2. Signál nám prostě "přetekl".

V případě Signed integer - je to ještě horší - představte si sčítání 7+1 tedy 0111 + 0001 = 1000. Neboli dekadicky 7+1 = -8, V obou případech pokud bychom si přetečení představili jako zvuk - patnrně by ten prudký skok signálu zněl v repráku jako "prásknutí" - až by se nám protočily bubínky. To je samozřejmě nežádoucí, proto inženýři vymysleli "Saturační aritmetiku". Ta si bere základ z analogového světa - pokud přebudíme zesilovač tak vám sinusovka něpřeteče na druhou stranu, ale zůstane pěkně ořezaná - jak to vidíme na obrázku.

Z hlediska satrurační aritmetiky - pokud počítáme 9+9 z našeho příkladu - výsledek bude 15 a pokud počítáme 15 + 9 výsledek bude zase 15. "Saturace" znamená nasycení - a na příkládcích je myslím docela vidět co tím autor myslel.

V satrurační aritmetice se vám signál ořízne jako v reálném analogovém zpracování - což je lepší než přetečení . Drobným problémem je, že až na specializované DSP procesory AVR, PICka, ARM, Intel, ani další komerční procesory satrurační aritmetiku nepodporují na hardwarové úrovni. Pokud výpočty se saturační aritmetikou programujeme softwarově - znamená to, že po každé operaci musíme výsledek kontrolovat na přetečení a pokud přetečení nastalo - musíme místo přeteklé hodnoty dosadit povolené minimumu / maximum.

Jelikož jazyk C vůbec přetečení nezná - berte jako fakt, že každý procesor má dva bity jménem CARRY a OVERFLOW které nastaví pokud při aritmetických operacích k přetečení došlo.

Potom vypadá každá matematická operace takto

Nebo pro odčítání

Tohle platí pro UNSIGNED integer - kde nám přetečení indikuje CARRY bit a OVERFLOW bitu si vůbec nevšímáme. To samé pro SIGNED Integer a 8 bitovou hodnotu :

Nebo pro odčítání

U SIGNED integerů nám přetečení indikuje OVERFLOW a zase si nevšímáme CARRY.

Jak to naprogramovat v C ? Opravdu nevím - já bych to pogramoval v AVR Assembleru takto.

Jak to naprogramovat v C bych nechal na místní guruy přes vyšší programovací jazyky - třeba na to je nějaká knihovna, jelikož všechny numerické algoritmy spěchají - zatím jsem je programoval jenom v assembleru a žádnou knihovnu pro C jsem nepotřeboval.

Takže tolik jednoduchá a přitom celkem neznámá věc se saturační aritmetikou - zbývá už jenom tradiční rada pro brunety - začíná podzim a bude chladno - ale minikraťásky s legínami - zaujmou skoro stejně jako minikraťásky na holém zadku.

Přestože se to nezdá, pořád se v "Matematice pro roboty" pohybujeme v brutálně zjednodušeném světě. Měříme napětí AD převodníkem a předpokládáme, že z něho lezou smysluplná čísla, ty pak proženeme algoritmy psanými v C a doufáme, že kompilátor ošetří všechny zákeřnosti.

Takže končí legrace a začínáme přitahovat šrouby, protože "ďábel se skrývá v detailech". Slabším povahám opakuju znovu a stále - šetřte své nervy a vyhoďtě si mně ze záložek dříve než to bude horší než ve škole - já nejsem zoufalec co touží po návštěvnosti svého blogísku, píšu jak umím a co umím nikoliv více, ale nikoliv méně.

Tedy - jedno z přechodzích zjednodušení bylo toto : psal jsem všude "svět celých čísel" ale ono to byl svět "celých kladných čísel" neboli svět "přirozených čísel" - když jsme počítali napětí baterky tak nikdo nepředpokládal, že procesor pojede při totálně zničené baterce s napětím -1V tudíž ani otázka měření záporných napětí nebyla na pořadu dne. Nicméně opakuju stále znovu - není nic lepšího než mít sonary s přímou digitalizací bez usměrňovače - a (ultra)zvuk je prostě střídavý signál Ať chceme nebo nechceme.

Takže ultrazvukový mikrofon nám produkuje signál od +XXX uV do -XXXuv což nám předzesilovač zesílí na nějaké rozumné milivolty a pak převede na AD převodník procesoru - je to tak ?

Není - vtip je v tom, že používáme operační zesilovače, které kdysi pracovaly se symetrickým napájením a dneska pracují s "virtuální zemí". Kvůli maximálnímu rozkmitu se napětí virtuální země dává rovno polovině měřícího rozsahu AD převodníku a všechny střídavé signály jsou pak součtem skutečného signálu a stejnosměrného napětí této "virtuální země".

No jestli jste z toho jeleni tak píšu jednoduše - AD převodník v AVR nebo PICce měří od 0 do 5V - tudíž nemůžeme měřit napětí -2V ale múžeme napětí -2V sečíst s konstatntím napětím virtuální země, kterou umísítíme do středu napájení takže -2V signálu je -2 + 2,5 = 0,5V na vstupu AD převodníku.

Takže když si v procesoru hrajeme na sinusovku která nám (v 8 bitovém rozlišení) kmitá od +127 do -128 (hodnot AD převodníku) - tak ve skutečnosti z AD převodníku leze sinusovka 0-256 honot - a signálu 0 voltů odpovídá hodnota 128 - Teoteticky !!!.

Jenomže ďábel se skrývá v detailech - takže co když virtuální zem není udělaná tak precizně aby měla napětí přesně 2,5 V - nebo není tak docela stabilní a někam nám ujíždí (třeba kvůli tepelné nestabilitě napěťové reference) ?

Jaké jsou naše možnosti

AD 1. Základní informací o signálu je amplituda, kterou spočtete jako

tedy je to vlastně numerický ekvivalent usměrnění - bez toho budete všechny algoritmy psát extra pro kladnou a extra pro zápornou půlvlnu - což je zjevná kravina a příliš vysoká cena za vyhnutí se potížím s driftem střední hodnoty.

AD 2. Zcela legální varinata, v některých případech však vadí, že stav "bez signálu" pak není hodnota 0 z ADC - typicky to vadí třeba při kompresi a dekompresi zvukových signálů.

AD 3. Zcela legální varianta - akorát v některých případech ve stavu bez signálu je střední hodnota jiná než ze signálem - takto vzniklá chyba má stejné účinky jako v bodě 2.

AD 4. Střední hodnotu můžete spočítat jako klouzavý průměr všech hodnot - ten musí mít dostatečně dlouhou základnu takže třeba

Viz exponenciální klouzavé průměry - tato metoda je téměř dokonale odolná proti pomalému driftu střední hodnoty, ale u příliš rozkolísaných signálů - může sama začít s jistým zpožděním kolísat a signál nám zkreslit.

AD 5. - moje nejoblíbenější varianta - nutnou podmínkou je aby frekvence vzorkování byla celočíselným a nejlépe sudým násobkem frekvence sužitečného signálu. Příklad (už jsem ho popisoval) - Vzokrujeme na 4 násobku frekvence ultrazvuku - tedy na 160 kHz - tudíž každé periodě odpovídají 4 vzorky A, B, C, D, - z těc vytvoříme dva vzorky jako

Vtip je v tom, že pokud máme vzhorkovací frekvenci na 4x frekvence signálu - je jist騞e "ob jeden vzorek" bude signál posunutý o 180 stupňů a tedy to bude "opačná půlvlna" ať už je střední hodnota jakákoliv. JEdiný požadavek je aby drift střední hodnoty byl během 4 měření alespoň trochu konstantní - což není problém dodržet.

AD 6. Jediné "matematicky zcela korektní" řešení je - ukládat všechna měření do bufferu a střední hodnotu spočítat jako aritmetický průměr až nakonec. Tím, se opravdu zbavíte střední hodnoty bez ohledu na její drift - ale samozřejěm se tím dostanete do potíží s daty, která se na robota valí v reálném čase a taky je je třeba v reálném čase zpracovat a smazat.

Celé odečítání střední hodnoty, nebo "virtuální země" je vlastně něco jako převod čísla z "unsigned integer" na "signed integer". Ať už bychom počítali s jednou nebo s druhou variantou, vždy je při zpracování signálu řešit otázku co když nám signál přeteče takže jak se u 8 bitového zpracování postavit k výsledku "300" - jak na to probereme příště.

Dnes už zbývá jenom tradiční rada pro brunety - chcete aby vám miláček koukal do očí ? oblečte si tričko bez výstřihu a netvařte se , že to neděláte schválně.

Pokud jste podrobně studovali odkazy z minula, jistě jste zjisili, že mezi mnou a matematiky je jistý rozpor - klouzavý průměr dvou sousedních hodnot, který jsem označoval za N=2 označují matematici za filtr prvního stupně a označují jej N=1 - doufám že přežijete když zůstaneme u toho že moje čísla jsou o jedničku větší. Mimochodem další důvod nevykládat ve škole, co jste se zde dočetli.

Ačkoliv jsem matematiku kolem toho nikdy nestudoval, tak pokud máte prostý klouzavý průměr N sousedních prvků a máte vzorkovací frekvenci f tak tento filtr funguje jako dolní propust, který propouští frekvence menší než f/2N, pokud používáte exponenciální klouzavý průměr pak dělící frekvence je přibližně f/4N.

Když už jsem měl AVR assembler kolem těchto filtrů vypilovaný k naprosté dokonalosti, žačal jsem si s filtry hrát. nejenom že můžete prvky sčítat, ale taky odčítat a to nejenom sousední ale taky od sebe více vzdálené. K tomu pak potřebujete kruhové buffery. Pak jsem logicky odvodil jak udělat jednoduchou frekvenční propust - a to takto : Pokud hodnotu v bodě A odečteme od hodnoty v bodě B. - pokud je frekvence signálu rovná modré sinusovce, nebo jejím lichým násobkům - "vyšším harmonickým" (fialová sinusovka) - dostaneme signál s dvojnásobnou amplitudou, zatímco signály na jiných frekvencích jsou utlumené, nebo dokonce úplně potlačené (žlutá sinusovka). Kdybyste to potřebovali napsat matematicky takto:

kde k je polovina periody filtrovaného signálu v počtech vzorků. Tedy pokud potřebujeme při vrorkování 10 kHz filtrovat 1 kHz pak je to 10 vzorků na periodu a k=5 jasné ?

Vzhledem k tomu že na pravé straně rovnítka se nám nevyskytuje Y - tudíž výstup tohoto filtru neovlivňje jeho vstup - tudíž jste pochopili, že tento fitr je typu Finite impulse reponse.

Nicméně jeho filtrační účinnost není nic moc. A protože obecně exponenciální průměry / filtry (alias Infinite impulse response) jsou při jednodušší matematice účinnější než Finite impulse - tak jse začal experimentovat i s nimi a došel jsem ke "skoro geniálnímu" filtru jehož vstup vidíte modře a výsup fialově. Zde je vzoreček.

k je opět polovina periody. Všimněte si, že oproti minulé verzi tam přibyl jenom jeden člen navíc. Zajímavý je koeficient alfa - ten určuje míru přednosu "energie" z výstupu na vstup filtru. pokud je roven 1 - filtr se rozkmitá a nikdy nepřestane, pokud je menší než 1 - filtr se podobá analogovým filtrům ve starých rádiích "audionech", které pro zvýšení selektivity, taky malé množství signálu vracely na vstup - tak aby pracovaly "těsně pod bodem rozkmitání".

Že to funguje i pro zašumělé signály - vidíte na obrázku - amplituda šumu je stejná jako amplituda užitečného signálu, a přesto jej je filtr schopen detekovat. Protože u takto zašumělých signálů je výstpu filtru taky znešištěn šumem je za výstupem filtru ještě klasícký exponenciální klouzavý filtr, který modrou křivku pěkně "uhladí". Pokud byste si chtěli s filtry tohoto druhu hrát ZDE je původní excelový soubor, ze kterého jsem grafy generoval.

Jestli máte pocit, že jsme dneska nezabředli do žádné matematické teorie - není se čemu divit - toto vše jsem skoro jako Jára da Cimrman "objevil" sám. Pak jsem to použil pro filtraci signálů u mých pokusů s měřením vzdálenosti pomoci zvuku na slyšitelné frekvenci alias "Zvukarem" A pak ( konečně !!!) jsem zjistil, že matematici tyto filtry znají - jako tak zvané "hřebenové filtry". Případně jako tzv. CIC "cascaded integrator comb" filtry. První vrianta, kterou jsem popsal je tzv "feed forward" varianta, druhá "oscilující" varianta je "feed back" varianta - která má velmi úzká maxima propustnost - není div že dovede ze šumu ''vytěžit" signál i v nepříznivých podmínkách.

Samozřejmě je otázka, jestli bych se neměl stydět, že tohle je moje samo-domo pokusničení a né součást akademického vzdělání - osobně se za to nestydím - protože takhle jsem došel sice dosti daleko, ale nikoliv tak daleko aby se filtr tohoto typu nedal naprogramovat v AVR assembleru.

Jako obvykle dvě poznámky

1. čím více se koeficient "alfa" blíží 1 tím lépe filtr rozliší v šumu vlastní kmitočet, ale tím déle "dokmitává" - což je jenom čílsicová varianta koeficientu Q z klasických filtrů - filtry s vysokým Q dokonale rezonují, jsou vysoce selektivní, ale díky dlouhému "dozvuku" mají jen úzké pásmo propustnosti (dozvuk brání reagovat na rychlé změny signálu). Naopak filtry které mají nízké Q jsou daleko více "širokopásmové" propustí širší pásmo, ale na změny reagují rychleji.

přibližný vzoreček pro vztah Q a našeho koeficientu "alfa" je Q = 1/(1-alfa).

2. neuvádím žádné přiklady prográmků - protože předpokládám, že stejně budete všechno programovat v C a tudíž by můj AVR assembler nebyl pro vás zajímavý. Filtry jsou natolik nenáročné, že rozdíl výkonu mezi C a ASM nestojí většinou za tu práci. Místo progámků si prosdujte zmíněný příklad v XLS.

Zbývá už jenom rada paní Kubáčové novomanželkám - točí se váš mažel za cizími ženami a vás to štve ? Místo tichého zuření doporučuju úplně opačný postup - už z dálky musíte manželovi nahlas oznamovat: "Táto támhle jde fantastická kočka, žejo ?" Uvidíte, že mažel bude minimálně lehce zaražen ....

Miliardář a bojovník proti korupci Karel Janeček založil firmu, která je zdrojem jeho bohatství v roce 1995. Ta firma se jmenuje RSJ a zabývá se tím, že počítače řízené softwarem s umělou inteligencí obchodují na burzách po celém světě. Mnohem méně známé je, že stejnou ideu jsme s Ondřejem Bendou měli už o rok dříve než Karel Janeček (který je o rok mladší) a že jsme v roce 1994 začali experimentovat s obchodováním pomocí softwarových "agentů" řízených pravidly, které vybíraly "genetické algoritmy" - no prostě nebyl jsem vždycky programátorský neumětel, jako jsem teď ....

Proč je miliardář Karel Janeček a ne já ? Já jsem v té době byl máti z domu vykopnutý a nekonečnými zkouškami trápený medik, Ondřej Benda byl v té době student, kterého znechutily "dřistoprdy" na divadelní fakultě JAMU a na nás oba se podvodníci ve finanční sféře dívali velmi podezřívavě. Karel Janeček měl navíc nimbus geniálního "matfyzáka" - který má zakázáno navštěvovat kasina v Las Vegas - protože v nich - díky své genialitě - mnohokrát rozbil bank.....

Zdá se, že jsem odbočil, ale nikoliv, protože co jsou ceny na burze - data zatížená šumem. Jak se s nimi pracuje - pomocí klouzavých průměrů. Mně se například v roce 1994 velice líbila tzv. Bollingerova stuha - což je naprosto stejný klouzavý průměr, který jsme probírali minule. (Schválně si odkliněte ten link).

Druhou variantou Bollingerovy stuhy byl "Exponential moving average". Tedy exponenciální klouzavý průměr. Představte si že místo prográmku s kruhovým bufferem, který jsme si popisovali minule :

Napíšete jenom a pouze

Jednoduché jako facka na hodině matematiky ne ? V čem je tedy kouzlo ?

Vtip je v tom, že místo abyste průměrovali 10 sousedních hodnot, které musíte udržovat v kruhovém bufferu atd. Tak prostě novou hodnotu spočtete jako 90% starého výsledku + 10% nového měření.

Jak se takový exponenciální průměr chová - vidíte na obrázku. K objasnění používáme tzv. "Diracovu jednotkovou funkci" která ale má v bode 0 hodnotu nekonečno - s tím jsou trošku problémy - tak používáme její integrál (nepodstatné). Co je podstatné je tohle - po náhlé změně vstupu - fialový lineární klouzavý průměr - prostě klesá lineárně až se ustálí na nové hodnotě. Exponenciální klouzavý průměr se na začátku mění stejně jako lineární, ale přesné hodnoty nového vstupu nikdy nedosáhne.....

Navíc - jak jste si jistě všimli tak exponenciální klouzavý průměr vnáší do signálu ještě větší zpoždění než lineární průměr. Nidky jsem to matematicky nestudoval, ale zkušednost říká, že lineárnímu klouzavému prměru 10 sousedních prvku (tedy N=10) odpovídá exponenciální klouzavý průměr přibližně poloviční síly tedy N=5.

Že si úplně nevymýšlím vidíte na obrázku - Všimněte si "zázračné" shody žluté a fialové křivky. Tedy v praxi téměř vždy místo otravování se s kruhovým bufferem pro 10 hodnot stačí spočítat něco jako

Mimochodem když jsme mluvili o "síle" exponenciálního klouzavého průměru doufám že jste pochopili, že exponenciální průměr síly (stupně N) se počítá jako

tedy

N = 2 .... Y = (Y+X) / 2

N = 3 .... Y = (2*Y+X) / 3

N = 4 .... Y = (3*Y+X) / 4 atd ....

Proč jsem jako programátor v Assembleru klouzavý průměr tak miloval ?

No pokud si zvoíte N jako mocniny 2 tedy 2, 4, 6, 16 atd pak v assembleru počítáte klouzavý průměr třeba pro N=8 takto

Tedy tak složitou věc jako EXPONENCIÁLNÍ kouzavý průměr počítáte bez jediného násobení, nebo dělení - zajímavé ne ? Už rozumíte proč jsme v přechozích dílech tak drilovali násobení a dělení bitovým posuvem ?

Ještě než skončíme - dovolím si vám prozradit informaci, které žádná žena neodolá: Klouzavé průměry jsou totéž co dolní propusti v numerickém zpracování signálu (DSP algoritmech).

Exponencíální klouzavý průměr je naprosto přesně totéž co RC dolní propust z analogové elektroniky a "vědecky" se mu říká "Infinite impulse response filter" neboli "filtr s nekonečnou impuslní odzevou". Lineární klouzavý průměr nemá svůj ekvivalent v analogové elektronice - nicméně numerickému filtru tohoto typu se říká "Fininte impulse response filter" - tedy něco jako "filtr s konečnou impulsní odezvou".

Schválně si proklikejte odkazy - abyste viděli jak "složitou matematiku" jsme dneska probrali. Myslím, že tak složitou, že pokud se dostatečně ledabyle zmíníte o tom, čemu rozumíte před vaší potenciální kořistí, žádná žena "která za to stojí" vám neodolá a dopadnete jako já - takže pozor !!!

Nezbývá než několik poznámek na závěr:

Exponenciální klouzavý průměr napodobuje RC fitry tak důkladně, že se může při špatném nastavení i rozkmitat (schválně si to zkuste pro N = - 2)

Obsah této kapitoly prosím naprogramujte do svého robota, ale rozhodně jej nevykládejte nikde ve škole - robot vám bude fungovat, ale já vaše studijní výsledky vaším sdělovat nebudu - pěkně se to naučte i se všemi integrály Tau a Epsilon - jak to máte v těch odkazech.

Zbývá už jenom rada paní Kubáčové novomanželkám - Vysoké podpatky, krátké sukně, dlouhé vlasy - to všechno miláčka dovelo rozvášnit před svatbou - teď k tomu přistupuje i umytá podlaha, vyžehlené prádlo a uvařená večeře - vidíte jak vaše možnosti po svatbě stoupají ?

Už kdysi dávno v článku o "Analogové logice" jsem zmiňoval, že robot, který se rozhoduje na základě pouze těch posledních měření dat z čidel má zaděláno na problémy způsobené šumem v těchto datech. Už tenkrát jsem doporučoval průměrovat, průměrovat, průměrovat.

Aritmetický průměr je dětsky jednoduchá matematická operace, která se učí snad někdy na prvnim stupni takže by se zdálo, že ani není o čem psát. Protože, jako vždycky, se "ďábel skrývá v detailech" je od průměru ve 4. třídě k průmměru ve firmwaru robota na Robotickém dni přece jenom nějaká ta cesta.

Zásadní problém průměrování v robotech je, že nemáme nikdy k dispozici všechna data. průměrování v robotech totiž nefunguje jako na cvičení z matematiky - kdy dostaneme tabulku se všemi daty a počítáme jak se nám zlíbí. V robotech na jedné straně čidla neustále chrlí nová a nová data a na druhé straně ať máme paměti jakkoliv mnoho - jednou prostě paměť dojde a budeme muset stará data zahazovat. Algoritmus pro půměr v robotovi tudíž musí být tzv. "proudový" od anglického Stream - proud. Tedy napsaný tak, že s každým měřením přijde jedna hodnota na začátek "pásu" a na konci pásu vypadne jeden výsledek.

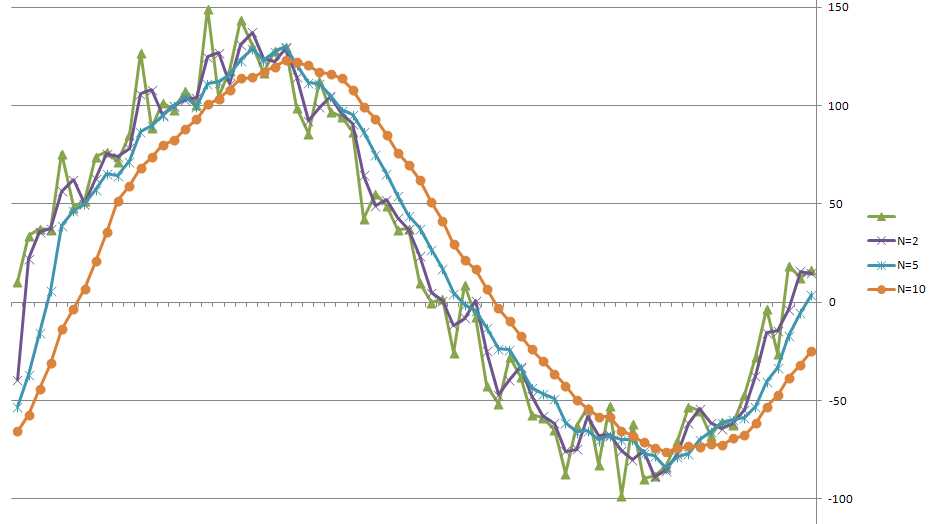
V případě průměrů těmto nárokům nejlélpe vyhovují tzv - klouzavé průměry. O co se jedná je vidět z obrázku - původní "zašumělá" data jsou zelená, a ostatní křivky jsou klouzavé průměry pro 2, 5 a 10 sousedních hodnot. Takže klouzavý průměr pro 5 hodnot se spočte tak, že (až se nám algoritmus ustálí) - třeba hodnotu č. 100 spočteme tak, že spolu sečteme hodnoty 100, 99 , 98 , 97 , 96 a vydělíme 5. Jednoduché, ale zase to zavání potřebou ukládat si do tabulky všechny naměřené hodnoty. To ve skutečnosti není potřeba, což si ukážema na nejnaivněji napsaném algoritmu pro "proudový" klouzavý průměr jaký lze napsat - budeme počítat klouzavý průměr pro 3 sousední hodnoty X je vstup, Y je výstup.

V pseudokódu by to bylo nějak takto

Myslím, že je to jasné, - původní hodnoty pomocných proměnných A, B, C jsou vlastně poslední 3 měření, které se na začátku každého cyklu posouvají tak, že hodnota A se zahodí do ní uloží hodnota B, do té se uloží hodnota C do prázdného C se uloží poslední měření a spočte se průměr.

Pro 5 a více proměnných je tento algoritmus hrozivě neefektivní proto se často používá pro minulé hodnoty tzv "kruhový buffer" pole hodnot, s ukazatelem na poslední hodnotu. představme si třeba buffer o velikosti 10 a počítáme klouzavý průměr posledních 10 hodnot.

Veškeré inicializace proměnných jsem samozřejmě vynechal. Vtip je v tom, že algoritmus už vůbec nepřipomíná sčítání sousedních hodnot. Představte si že proměnná POSLEDNI obsahuje hodnotu X z doby před 10 měřeními a proměnná SUMA obsahuje součet všech posledních 10 měření - takže pokud uděláme operaci SUMA = SUMA - POSLEDNI (odečteme 10 měření starou informaci) a když pak uděláme SUMA = SUMA + X tak přičteme nejnovější měření a tím se nám součet obsažený v proměnné SUMA o 1 měření "posune" vpřed.

Pak staré X uložíme do BUFFERU a hodnotu indexu i zvětšíme o 1 aby ukazovala na novou hodnotu. Pokud i je větší než velikost bufferu musíme i vrátit zase na začátek.

Samozřejmě že bychom mohli celý průměr počítat i naivně z hodnoty proměnné BUFFER jako

Y = ( BUFFER [1] + BUFFER [2] + .... BUFFER [10] ) / 10 ale to by bylo skoro stejně neefektivní jako posouvání hodnot ve stylu A=B, B=C, C=D atd ...

Pokud budete tento algoritmus programovat v Assembleru (nebo i v C) je výhodné používat buffer velikosti mocnin 2 - 2, 4, 8, 16 hodnot. pak jetaky dobré prvky bufferu očíslovat od 0 třeba do 7, protože pak můžete poslední dva řádky

Napsat jako

neboli

neboli pro 16 hodnot

Poslední poznámka na závěr - s rostoucím počtem půměrovaných hodnot - klesá šum v datech - toho jste si jistě všimli na grafu. Je však nutno výslovně poznamenat, že s tím zároveň roste zpoždění, které do změn v datech průměr zanese. Nikdy jsem to příliš matematicky nestudoval ale zpoždení odpovídá přibližně polovně průměrovaných hodnot - tedy pokud průměrujeme 10 sousedních hodnot - dostaneme výsledky, které se oproti původním datům opožďují o 5 měření - pokud počítáte předem známé hodnoty z tabulky tak je vám to jedno, ale u robota nikdy "nevidíte do budoucnosti" - nezískáte budoucí měření - takže vám nezbyde než s touto neodstranitelnou vlastností klouzavého průměru počítat ...

Zbývá už jenom rada paní Kubáčové pro novomanželky - že miláček prdí před vámi už dlouho - to je známkou jeho důvěry ve vás, ale pokud vy začnete po svatbě prdět před ním - možná si bude mylně myslet, že se z vás stala novomanželka - čuně - takže mu ten systém vzájemné důvěry raději před prvním prdem vysvětlete...

Mám nepříjemný pocit, že jediný rozdíl mezi mým blogem a školou spočívá v tom, že ve škole je matematika častěji než jednou za týden, ale jelikož jsem 2/3 své bastlířské kariéry používal celočíselné algoritmy v assembleru - tak toho mám tolik na jazyku, že si mě raději vyhoďte ze záložek, protože nemám v úmyslu jen tak přestat.

Mimochodem jak byste spočetli 2/3 * A což takhle 22 / 33 * A neboli 22 / 32 * A neboli ( 22 * A ) >> 5 neboli - jak dále všechno převést na sčítání a bitový posun ?

Už minule jsme měli násobit 39,2 a vykašlali jsme se na to a násobili jsme místo toho 39. V tomto blogu popis mých potíží s měřením napětí pokračuje. TAkže minule jsme použili dělič 1 : 16 a AD převodník, který měří maxímálně do 2,56 V abychom změřili napětí až do 30 voltů.

Vše jsem si početl jako minule, naprogramoval a - ono to nefungovalo - tak jsem přeměřil hodnotu napěťové reference v procesoru (je vyvedená na pin AREF) a zjistil jsem, že napěťová reference není 2,56, ale 2,73 V což je ještě v normě, neboť Atmel pripouští, že referenční napětí se může pohybovat "od Šumavy k Tatrám"

Všechno je zapájeno, naroutováno, tak co teď - pokusíme se počítat napětí v milivoltech z hodnoty AD převodníku úplně přesně.

Takže máme napětí 2,73 a dělič 1: 16 - maximální napětí které odpovídá hodnotě 1024 10 bitového AD převodníku tedy je 2,73 * 16 = 43,68 V převedeno na milivolty 43680 mV.

Kdybychom postupovali jako minule tak bychom uvažovali čím budeme hodnotu AD převoníku násobit a došli bychom k hodnotě 43680 / 1024 = 42,65 - což bychom mohli zaokrouhlit na 43.

Řekl jsem ale, že spočteme napětí úplně přesně pokud tedy hodnotě ADC = 1024 má odpovídat hodnota NAPETI = 43680 což takhle na to jít stylem

Ano - takhle je to správně, ale chce to ještě učesat.

1. násobit 40 000 a pak dělit 1000 to zavání přetečením mezivýsledku, takže nejprve všechno vykrátíme na nejvyšším společným dělitelem - hodnotu 32.

Pak doplníme všecno zaokrouhlování, bitové posuny a tak

A máme to spočteno maximálně přesně, stejně přesně jako kdybychom počítali s reálnými čísly a skutečným dělením.

Následuje obvyklá kapitola poznámek - kde má celý postup čertovo kopýtko ? Především v tom, že násobíme 1024 * 1365 - přetečení 16 bitového mezivýsledku tedy není možnost, ale jistota. Musíme tedy použít 32 bitový mezivýpočet - proměnnou typu uint32_t.

Tím je jasné, že nemá smyslu ani násobit pomocí bitových posunů jeden bitový posun 32 bitového čísla je kompilátorem přeložen jako 4 bitové posuny 8 bitové hodnoty, takže (aleposň u AVR) je rychlejší rovnou násobit. pokusím se napsat vzorovou proceduru

Znalcí jazyka C asi křičí - kde je přetypování mezivýsledku na 32 bitů ? Není potřeba (doufám), protože už vstupní hodnotu ADC jsem deklaroval jako 32 bitovou, ačkoliv hodnota z AD převodníku bude mít jen 10 "platných" bitů . Upřímně jako bývalý programátor v Pascalu se přetypovávání smrtelně bojím - a v C, kde číslo přetypujete na pointer a zpět - dvojnásob.

Předpokládám, že právě si říkáte - měsíc žvanění a výsledkem je procedura na tři řádky - s lehkou ironií vám odpovídám - na tři řádky, ale jak sofistikovaná ;-)).

Zbývá už jenom oblíbená rada paní Kubáčové pro novomanželky : pokud máte manžela, co neumí do pětí napočítat a slibujete si od toho, že vám to nespočítá - nemylte se - právě tyhle typy vám to bez slitování spočtou do posledního zrnka.

Už když jsem já byl prvňáček, za hlubokého bolševika, tak paní (soudružka) učitelka Habrnálová se v matematice vždycky přikrčila zkontrolovala jestli někdo není za dveřmi, a pak šeptala - měli byste to počítat podle vzorečku, ale já vás to naučím trojčlenkou.... Tedy už tehdy byla trojčlenka zakázaná, co teprve dneska když nad nami nebdí laskavé oko Sovětského Svazu, ale ještě laskavější oko Evropského Svazu - pardon - Evropské unie.

Tedy z nedostatku jiného popisu označuju jako trojčlenku úlohy typu

Neboli babička na obalení 5 řízků potřebuje 3 vajíčka, kolik bude potřebovat na obalení 7 řízků ?

Neboli A₁ / 7 = 3 / 5 neboli A₁ = 7 * 3 / 5 neboli 4,2 vajíčka... Jasné ?

Takže si probereme úlohu na trojčlenku v mých robotech - napětí na motorech, které může dosahovat až 30 voltů se měří 10 bitovým AD převodníkem s vnitřní referencí 2,56 V.

Takže nejprve z pohledu konstruktéra - napěti 30V musím měřit AD převodníkem s maximálním napětím 2,56 V - jaký zkonstruuju dělič ? Takže 30 / 2,56 11,78 - hnusné číslo - a protože v oblasti nad 10 se z normálních odporů nejlépe sestavuje dělič 1:16 tak bereme dělič 1 : 16 čímž budeme moci měřit napětí až 2,56 * 16 = 40,96 V

A teď z pohledu programátora. Už jem psal - pro napětí používejte nějaké "lidské" jednotky takže přepočteme číslo z AD převodníku na milivolty -tudíž bude nabývat hodnot 0 - 40960

10 bitový AD převodník má max hodnotu 1024 takže musíme změřenou hodnotu násobit koeficientem 40960 / 1024 = 40

X * 40 je X * 32 + X * 8 takže konečný výpočet bude

Samozřejmě, že proměnné NAPĚTÍ i ADC musí být typu uint16_t, který má maximální hodnotu 65535 jinak by byl problém ( což by byl i s proměnnou typu int16_t, která je od - do + 32767).

Jenom drobná poznámka - víte jak vypadá dělič 1 : 16 - od pinu procesoru do země jde odpor 1K a ke zdroji signálu jde odpor 15 K jasné ?

Tohle bylo až příliš jednoduché, takže si dáme druhou variantu - místo vnitřní reference 2,56V použijeme napětí procesoru 5V jako referenci.

Takže nejprve dělič 30/5 = 6 - dělič 1: 6 nedáme z normálních odporů nidky dohromady tak použijeme můj oblíbený 1 : 8 - ten se staví tak že do země jde odpor 470 ohm a ke zdroji signálu jde odpor 3300 ohm - jenomže to není zcela přesně 1: 8 ale 1: ( 3300 + 470 ) / 470 to je 1 : 8,0213. Takže při referenci 5V změříme AD převodníkem maximální napětí 8,0213 * 5 to je 40,1 V.

Tudíž by bylo nejlépe násobit 40100 / 1024 to je 39.2 což můžeme brát jako 39 a tedy

Pro veliký úspěch třetí pokus: Představte si, že necháme dělič 1: 16 z 1 příkladu, ale použijeme referenci 5V z druhého. To nám dá maximální napětí 5 * 16 = 80 V - Musím psát vzorec ?

Ale jo 80 je 64 + 16

Tato varianta však má problém - pro napětí nad 65 voltů hrozí přetečení výsledku, protože náš datový typ uint16_t zpracuje max 65535 milivoltů.

Doufám, že se necítíte uraženi matematikou pro 3 třídu základní školy, tak přidávám radu paní Kubáčové pro novomanželky : Ačkoliv my se učíme počítat s celými čísly - vy se naučte velice dobře počítat s desetinnými, protože pokud řeknete - miláčku moh bys zvýšit svůj příjem 1,2 krát - váš miláček se nad tím hluboce zamyslí - zatímco když řeknete - zvyš svůj příjem 8x - zasměje se a místo peněz - patrně uteče k milence...

Hodnocení domácí úlohy z minula

Pětku mají ti, co nevymysleli nic

Čtyřku mají ti co vymysleli 127*X = ( X << 6 ) + ( X << 5 ) + ( X << 4 ) + ( X << 3 ) + ( X << 2 ) + ( X << 1 ) + X

Trojku mají ti, kteří si uvědomili, že takový výpočet je pomalejší než prosté 127 * X = 127 * X, tedy obyč. násobení

Dvojku mají ti, kteří to vyřešili tak jako já tedy 127 * X = ( X << 7 ) - X

Jedničku mají ti, kteří přišli na něco ještě lepšího.

Dostáváme se k bolestivé otázce dělení, které je pomalé a hlavním zdrojem chyb. Proto jak už jsem psal mockrát se mu snažíme vyhnout jak jenom to jde.

Především aritmetický bitový posun doprava je ekvivalentní dělení mocninou 2 takže dělit

2, 4, 8, 16, 32, 65, 128, 256, atd je velice snadné a rychlé, dokonce tak snadné a rychlé, že si můžeme dovolit akceptovat i nějakou tu drobnou chybu třeba X / 30 můžeme napsat jako X >> 5. Pokud by takto vznikla veliká chyba třeba pro X / 11 můžeme nejprve násobit a pak dělit takže X / 11 = 3 * X / 33 to je přibližně 3 * X / 32 = ( 3 * X ) >> 5 = ( X << 1 + X) >> 5

Pokud budeme nejprve násobit - je třeba si dát pozor na přetečení výsledku.

Poslední problém - je otázka zaokroulování - celočíselné dělení stejně jako bitové posuny prostě odříznou desetinnou část takže 3/4 = 0 a hotovo stejně tak 3>>2 = 0 takže pokud počítáme můj první příklad A = 3 * X / 4 je třeba zaokroulovat, což provedeme tak jak sme to dělali s reálnými čísly ve starém dobrém basicu na IQ 151

Problém je v tom co je v naší celočíselné matematice to 0,5. Nebo to zase takový problém není dělíme li 8 je 0,5 * 8 = 4 takže A = X / 8 vypočteme jako

Zkouška 5/8 = 0,625 zaokrouleno 1 .... (5+4) >>2 = 1. Takže si prosím zapamatujte jako pravidlo, že zaokrouluje se takto

ATD. Pokud dojde k té něšťastné události, že prostě budete muset dělit celočíselně, funkcí pro dělení, což se snadno stane třeba když nedělíte konstatntou ale proměnnou pak

X = A / B se se zaokrouhlováním počítá jako

Kde jako DIV zase označuju celočíselné dělení, jestli to váš programovací jazyk rozlišuje. Jestli vám to připadá složité - tak vězte, že součty a bitové posuny jsou neměřitelně malý strojový čas navíc proti času dělení a za zlepšenou přesnost to stojí.

Pro dnešek už zbývá jenom blondýnami (i brunetami) bedlivě očekávaná rada paní Kubáčové pro novomanželky : Ženy se často stydí za "nohu sedmičku" ale na "prsa pětky" jsou hrdé - vůbec to tak neberte - každé číslo se nakonec v posteli srovná !

Minule jsem napsal 9 zásad celočíselné matematiky v robotech, aniž bych přitom vysvětlil hlubší smysl (jako obvykle). Takže dnes si dáme hlubší smysl a pokračování.

1. Tedy pokud počítáte jen s celými čísly jsou operace, které nezhoršují přesnost výsledku jako je násobení a sčítání / odčítání.

2. Pak je dělení, které naopak v celočíselné verzi výrazně snižuje přesnost výsledku

3. Proto musíme zaokroulovat.

4. Navíc u celočíselných výpočtů záleží na pořadí operací.

3 * 10 / 4 = 7,5 zatímco (3 * 10) DIV 4 = 7 zatímco 3 * (10 DIV 4) = 6

matematici by řekli že celočselné dělení (mnou označené jako DIV) není asociativní a distributivní, ale to už moc smrdí školou, takže rychle dále.

Kromě naznačených problémů s přesností jsou i problémy s rychlostí výpočtu .

1. Sčítání a bitové posuny jsou nejrychlejší

2. Násobení je výrazně pomalejší a to i u procesorů s hardwarovou násobičkou jako jsou Atmely AtMega.

3. Dělení je nejpomalejší.

Z toho vychází mé oblíbené způsoby výpočtu

2*X = X+X nebo X << 1

4*X = X << 2 ( v tomto případě je X+X+X+X už výrazně pomalejší)

8*X = X << 3 ( a tak dále - myslím že násobení mocninami 2 je vám jasné)

5 * X = 4*X + X = (X << 2) + X

10 * X = 8*X + 2*X = (X << 3) + (X << 1)

A tak dále. Řeknete si - necháme tyto optimalizace kompilátoru "ten má větší hlavu". V tom případě možná odevzdáváte úspěch svého robota do rukou nějakému Indovi, který nedopsal pořádně optimalizace, protože jeho šéfík - zchudlý maharadža - strašně spěchal, protože už núúúútně potřeboval prachy.

Za domácí úkol máte spočíst bitovými posuny 127 * X.

Zbývá už jenom rada paní Kubáčové pro novomanželky : Někdy se matematickým zpracováním dat jistá informace ztratí - číslo 240 například rozhodně nemá na manžela takové účinky jako 90 + 60 + 90 žejo ....

Minule jsem se poněkud rozkecal, nicméně ani dneska si nemohu teoretický úvod odpustit. Pokud budete chtít nahradit počítání s reálnými čísly počítáním s celými čísly a zadáte si nějaké vhodné heslo do Googlu - určitě vám vyskočí odpověď "Fixed point aritmetics" - neboli "aritmetika v pevné řádové čárce".

Až to nastudujete - zistíte, že je to primitivně jednoduché - prostě 32 bitové číslo rozdělíte tak že vyšší 3 byty jsou celá část a nejnižší byte je desetinná část a hotovo - není co řešit. Tuto variantu budeme taky probírat a nic proti ní, ale někdy je to "kanón na vrabce" a někdy naopak to vůbec neřeší váš problém.

Příklad : zadejte 15.3 V ve vaší matematice: bude to něco jako 15,3 * 256 = 3917 - absolutně zmatené číslo. Já vám poradím - kašlete na fixed point a zadávejte napětí v milivoltech - pak to bude 15 300. Není to lepší s menší možností fatální chyby ?

Proto bych si nejprve dovolil probrat počítání s celými čísly - bez fixed point aritmetiky - a až pak s ní.

Takže dáme si seznam zásad podle kterých pojedeme:

Zásad je určitě ještě více, ale protože nechci aby polovina mých čtěnářů utrpěla migrénu a ta druhá krvácení do mozku - pro dnešek zase končíme. Přemýšlejte nad mými 9 body, a jestli objevíte ještě další (a pište si, že jsou ) sem s nimi do komentáře, ať si zasloužíte pochvalu od "dědka", který pochvalami rozhodně neplýtvá.

Zbývá už jenom rada paní Kubáčové pro novomanželky : Lodičky za 4999 + kabát za 6999 + šaty za 2999 + kabelka za 1999 + kadeřník za 2499 + PIN manželovy kreditky = rozvod - je vám tato rovnice jasná ?